A Simple Basic Causal Macro Impact Model

 

George E. P. Box (1919-2013) was a statistician at the University of Wisconsin--Madison.

Economists are having trouble with macroeconomic models (I posted about the topic here). Macroeconomic modeling got off track by requiring that models have micro-foundations based on expectations, meaning that macro-societal economic forces had to be derived from the individual decisions of economic agents, for example, you and me buying groceries. Unfortunately, there are lots of different ways expectations can be formed (rational expectations, model-consistent expectations, adaptive expectations, etc.)  From the perspective of macro Systems Theory, micro-foundations make a logical category error. "Expectations" are not an attribute of macro-systems but of economic agents. The decision has led to a dead end in macro-economic modeling.

Having a solid basis for macro-modeling makes all sorts of sense. You would like the causal foundations of your theories to be true by definition.* Actually, there are three causal models that macro-economics could be based upon, that is, used to derive other, more complicated models.  They are the Kaya Identity, the Solow-Swan Model of economic growth**, and the AD-AS (Aggregate Demand-Aggregate Supply) Market Model.

NOTES

* In logic, a statement that is true by definition is a tautology.

** Actually, the Solo-Swan model can be derived from the Kaya Identity, so we really only need two models.

Code

If you would like to run the R program in your web browser, cut and paste the following code into the editor window at https://rdrr.io/snippets/.

Kaya <- function (time=100,N=100,n=1.4,L=50,Q=100,q=1.04,CO2=1,
Temp=1,l=.5,e=.75,c=.0002,t=.0001,limit=1) UseMethod ("Kaya")
Kaya.default <- function (time=100,N=100,n=1.4,L=50,Q=100,q=1.04,CO2=1,
Temp=1,l=.5,e=.75,c=.02,t=.01,limit=1) {

TEMP <- matrix(0,time,1)
TIME <- matrix(0,time,1)
for (i in 1:time) {
N <- N * n;

L <- N * l;
Q <- Q * q + L * e;
CO2 <- Q * c;
Temp <- CO2 * t;
TEMP[i,1] <- Temp;
TIME[i,1] <- i;
if (i > time/2) {c <- c * limit}
}
plot(TIME,TEMP)
}
par(mfrow=c(2,2))
# Sample Function Calls
Kaya(n=1.03,q=1.04)
title(main="Exponential")
Kaya(n=.9,q=1)
title(main="Asymptote")
# De-Growth
Kaya(n=.9,q=.9)
title(main="Degrowth")
# Decline
Kaya(n=.6,q=.6)
title(main="Decline")
Kaya(n=1.03,q=1.04,limit=0.95)
title(main="IPCC Slow")
Kaya(n=.9,q=1,limit=0.95)
title(main="IPCC Fast")

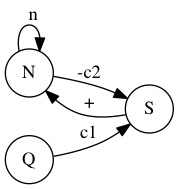
The Malthusian Controller

There are lots of versions of the Malthusian Model. Understanding the model, which is very simple (see the directed graph, DG, above) is complicated by all the verbal expositions and criticisms of the model (Marx called it a "stain on the human race"). The model basically says that if the means of subsistence (production, Q, in the DG) does not expand as rapidly as population (N, in the graph above) then the Standard of Living (S) will decrease eventually creating a Malthusian Crisis.

From the standpoint of World-Systems Theory and Cybernetics, the Standard of Living (S) is the Malthusian Controller that keeps population growth in check. Although populations in Western Core Countries have had little or no experience with Malthusian Crises, the Malthusian model is still applicable to historical situations and may, in the future, become applicable to Western societies if Climate Change reduces Q.

You can run R-code to experiment with the Malthusian Model here and produce the time series plot above with shock decomposition. The model is taken from Germany after Unification in 1871 when there was a brief Malthusian crisis.

Notice that after 1890, a Malthusian Equilibrium is reached when population and production are in balance.

Where are all the Alien Super-Civilizations?

Scientific American just published a very significant article titled Alien Super-civilizations Absent from 100,000 Nearby Galaxies. The article reports that "the most far-seeing search ever performed" looking the artifacts that would be produced by advanced Super-civilizations has come up empty handed. This might seem like an interesting piece of scientific trivia or even science fiction, but the reason for this "null result" has important implications for how we develop models of our own World System. It suggests that our preconceptions about how civilizations develop are "deeply flawed".

The new study by Pennsylvania State University astronomer Jason Wright used a new approach to searching for alien civilizations. Instead of conducting a traditional SETI survey looking for electronic messages from the stars, Wright looked for the thermodynamic consequences of galactic-scale colonization. Think about this point carefully (physicist Freeman Dyson did in the 1960's): a growing, advanced, energy-hungry technological culture would ultimately be limited by access to energy. In the current age of Peak Oil (or even after the 1973 Arab Oil Crisis), we shouldn't be surprised by this limit to growth, but our current neoclassical economic growth models contain no such limits.

A truly advanced civilization, when faced with limits to growth imposed by decreasing supplies of energy, would be capable of taking extreme measures such as harvesting energy from surrounding stars using Dyson Spheres. The important point here is that Dyson Spheres or any other advanced technology for harvesting energy would leave a mid-infrared glow of radiated heat waste. Astronomer Jason Wright, after examining 100,000 nearby galaxies, found no evidence for large-scale radiated heat waste that would signal the existence of Super-Civilizations.

The possible reasons for the null result are extremely important:

• Possibly, advanced technological civilizations always self-destruct. In the 13.8 billion years since the Big Bang, civilizations such as ours have come and gone, collapsing from energy limits, environmental damage, nuclear war, etc.
  
• Possibly, any sufficiently advanced, successful technological civilization would be indistinguishable from Nature (a position originally argued by science fiction author Karl Schroeder). Successful advanced civilizations would be more integrated with their natural environments, slower growing (even Steady-State systems), striving for technological efficiency and coming ever-closer to thermodynamic equilibrium.

Current neoclassical economic growth models predict exponential growth forever without limits to growth imposed by energy depletion. They predict the eventual construction of Dyson Spheres or some other technology to harvest energy from surrounding stars. They predict the existence of mid-infrared glow from radiated heat waste. These predictions have failed and it is time to consider neoclassical economic growth models as also having failed.

In future posts I will investigate alternative models that should now be given more serious consideration as replacements for neoclassical economic growth models.

The Steady State Economy: Realistic Model or Illusion?

The idea of a steady state economy has a long history. It was discussed by Adam Smith, John Stuart Mill, John Maynard Keynes, Nicholas Georgescu-Roegen, E.F. Schumacher,  Kenneth Boulding, and Herman Daly (all discussed here). Basically, the theory of economic growth describes the conditions under which an economy will grow (I've discussed the neoclassical growth model here) and steady-state economy theory describes the conditions under which the economy will stop growing (without collapsing). Both of these theories are flawed for reasons described by the theory of complex dissipative systems. I'll introduce some of these ideas in this post, but my major objective is to introduce the concept of steady state.

The fundamental insight from the steady state economy model is displayed in the graphic above taken from Herman Daly's (1977) Steady State Economics (San Francisco: Freeman) on page 35. Economic growth theory takes up the right-hand box in the figure. The economy, in Daly's view, produces stocks of artifacts (capital goods and stocks of knowledge) that not only deplete the Ecosystem (the left-hand box) but also generate pollution (even knowledge production does this, think of your University's power plant). Compared to the Ecosystem, which is open to Solar Energy and accepts heat pollution, the Economic system is closed. From my earlier discussion of economic growth theory (here), the economy is typically thought to be open to population growth and technological change. Daly includes both those stocks (the stock of population and the stock of knowledge) within the economic system.

If we split the drawing in half, the economy is open to input from the Ecosystem and the Ecosystem is open to pollution and depreciation from the economy as well as solar input.  The theory of open systems shows that only closed systems can reach a permanent steady state. An open system is always forced into another state by its inputs. So unless solar energy becomes an input to the Economy and, at the same time, regenerates the Ecosystem which is being depleted but the Economy, the combined system cannot reach a permanent steady state at a high level of economic development. Basically, the Second Law of Thermodynamics holds that all closed systems run down due to dissipation of energy (the theory of complex dissipative systems).

What is lurking under all this theory is the concept of openness. The subtleties are easier to understand by considering the general open system S(t) = A S(t-1) + B X(t-1) where t is time, S is the state of the system, A and B are matrices of coefficients and X is a matrix of inputs from the environment (the open part of the system). The characteristic behavior of the state-space representation is determined by properties of the A matrix, specifically its stability (all eigenvalues of A less than one). If the system is stable it will reach a steady state only when X becomes zero, that is, when the inputs are dissipated (think of X as the environment) or when X becomes a constant, that is, the environment reaches a steady state. If the system is unstable, it will growth forever, even without inputs--which is impossible. So, real world systems must ultimately become stable.

But, imagine a world which is radically open. There are all sorts of systems, some stable, some unstable (think of normal cells in the human body and cancer cells, the cancer cells are growing unstably). Each system is interacting with other systems. In this disorderly world, change over time is determined by the unstable systems. Unless the unstable systems are stabilized, they take over the stable systems. In the case of cancer cells, without killing the cancer cells (one type of steady state) they eventually kill the host system.

The view of the ecological system and the economic system advanced by the theory of steady state economics involves mildly open, stable systems. What if they are not? What if they are more like the human body? What if the Economy and the Ecological system are radically open? This will be a topic for a future post.

The theory of radically open systems possess serious problems for all attempts to specify the steady state or even the growth path of an economy. All the conclusions from economic growth theory, steady-state economic theory and simple open systems theory depend on being able to specify the state S of the system. In radically open systems, if the state is misspecified then some unmeasured, unstable force in the environment (e.g., a caner pathogen) can disrupt the system and make forecasting the future impossible. In a world of radically open systems, all systems are weakly state determined and strongly driven by the environment. For theorists and model builders, accustomed to specifying system states, specifying the entire environment is an impossible task. For us consumers of theories and models, we need an answer to the question of how open our real word systems are before we an have much faith in the conclusions of theoreticians and model builders.

The one question that the debate between economic growth theorists and steady-state economists has brought into the open is whether any of our economic systems are moving toward a steady state. And, if an economic system is moving toward a steady state (an empirical question) what might happen after that (a speculative question). The resolution of this question is important because it impacts the Ecosystem on which the Economy depends. I will present historical data from and test actual economics systems in future posts (something that is seldom done in ECON 101).

HISTORICAL NOTE

The concept of a Steady State Economy was dropped from ECON 101 after WWII as was much of what had been developed by Classical Economists in the Nineteenth Century (except David Ricardo).

For example, in the graph above is the output from a Steady-State Malthusian System model produced by the code below, if you would like to experiment yourself. Note, this model is a closed system.

Code

A Steady-state Malthusian Model. Models have a compact R-code in dse and can be run easily https://rdrr.io/snippets/. Cut-and-paste the following code into the Snippets editor window. When you run it, it should produce the shock decomposition diagram and the forecast in the graphic above.

#

#    MALTHUS

#

require(dse)

require(matlab)

f <- matrix( c(   .8, 0, 0.09478143,

               0, .8, 0.09238426,

                      0.000000000, 0.00000000,  1.000000000

),byrow=TRUE,nrow=3,ncol=3)

h <- eye(2,3)

k <- f[1:3,1:2,drop=FALSE]

TRM <- SS(F=f,H=h,K=k,

z0=c(0.09478143, 0.09238426, 1.00000000),

              output.names=c("N","QA"))

stability(TRM)

TRM

TRM.data <- simulate(TRM,sampleT=20,

,start=1,freq=1,noise=matrix(0,20,2))

TRM.model <- l(TRM,TRM.data)

#tfplot(TRM.model)

shockDecomposition(toSSChol(TRM))

tfplot(forecast(TRM.model,horizon=20))

Is Climate Change an Economic Problem?

In Chapter 3 of the Climate Casino, William Nordhaus argues that climate change is an economic rather than scientific problem (find my reviews of other chapters here). The argument is controversial. Heat waves, melting ice sheets, droughts, rising sea level, storms and record temperatures are typically thought of as a complex scientific problem. Prof. Nordhaus argues that the economic problem is more straightforward: the people that are dumping CO2 into the atmosphere don't have to pay for their emissions. If they did, they would be more careful about what they did with the by-products of burning fossil fuels. Economists call this an externality, that is, "...a by-product of economic activity that causes damages to innocent bystanders" (p 18). Because no one owns the atmosphere, not even government, there is no one to charge for its use and no market in which to purchase such environmental services. 

Economists like this argument; it shifts the debate from "who is to blame" to "who should pay" for damages caused by climate change. Unfortunately, polluters argue that no one is actually being harmed by CO2 emissions and that there is no observable link between CO2 emissions, climate change and economic damages. 

Prof. Nordhaus confronts these arguments by presenting the data and using models to predict the future. Since 1900, global CO2 emissions have been rising linearly (on a log scale) in his Figure 2 above (p. 21). Although there have been some interesting periods of acceleration (after WWII, for example), the general trend has been continuously upward.

Over the same period, there have been technological improvements that increased the efficiency with which fossil fuels are being burned. Technical efficiency has reduced the carbon intensity of, at least, the US economy as displayed in Figure 3 above (from page 22 of the Climate Casino, again presented on a log scale). This process is called decarbonization, but "...while the carbon intensity of production is declining, it is not declining fast enough to reduce total CO2 emissions, either for the world or for the United States" (p. 23). In other words, technological change will not get us out of this dilemma and neither will the substitution of renewable resources because they are more expensive than fossil fuels--returning us to the economic problem.

Another part of the economic problem is that the negative impacts of fossil fuel burning, even with increased technical efficiency in their use, will not be felt for many years in the future. To look out past 2013 when the Climate Casino was written into the future when environmental effects could become serious, we need a mathematical model that can make quantitative predictions. Prof. Nordhaus has such a model, called the DICE model, as in "roll the dice". In Figure 3 above (from p. 33 on the Climate Casino), emissions projections out to 2100 from the DICE model are compared to projections made by eleven EMF models from the Stanford University Energy Modeling Forum. The projections from the DICE model compare quite favorably with the average of the EMF models.

Prof. Nordhaus acknowledges that there is a great deal of "uncertainty" in these estimates. CO2 emissions in 2100 range from about 40 billion to over 130 billion tons per year. The differences in predictions have nothing to do with "chance" or "random events" but rather with the different structures and assumptions of the models. The models are totally deterministic. 

In the face of uncertainty about the future (and uncertainty about the models), Prof. Nordhaus makes the following suggestion:

Start with a best-guess scenario for output, population, emissions, and climate change. Take policies that will best deal with the costs and impacts in this best-guess case. Then consider the potential for low-probability but high-consequence outcomes in the Climate Casino. Take further steps to provide insurance against these dangerous outcomes. But definitely do not assume that the problems will just disappear. (p. 34-35)

This sounds reasonable, but the arguments in Chapter 3 of the Climate Casino do not seem well connected to the suggestion. Is Prof. Nordhaus saying that the DICE and EMF-22 models are necessary to making judgments about either the future or about policy actions that should be taken in the present? Are the DICE and EMF-22 models an accurate simplification of how the world economy works? How do we know that? Have the models been somehow validated? Is there a way we can check the projections being made by the models? If we are going to run policy experiments on the models, how do we know the world economy will respond in the same way? How would we even think about implementing policies that would have an impact on the world economy? Is there any way for us to evaluate these models as systems? What kind of confidence would we have to have in models to make predictions almost eighty years into the future? Is there any reason to believe that we can really predict that far into the future? And, how do the models prove that climate change is really an economic problem? As I will argue later, it seems more realistic to view it as a "system" problem, specifically a problem of the Capitalist world-system, a system that is great at exploiting environmental systems for profit. Is it possible to change this system? How have macro-societal systems changed in the past?

So many questions! They will all have to be topics for future posts, keeping in mind that this blog is about causal macrosystems and not about climate change. Unfortunately, it is in the area of climate change that the stakes are highest and to which, hopefully, researchers are bringing their best models!

EXERCISES

1. Download the DICE users manual (here). How well was the model validated? What evidence was offered to support using the model for policy experiments? How were the model parameters determined? Evaluate Ackerman's (2007: 1657 here) concern that "...the optimistic projections and modest optimal policies often attributes to models such as DICE may be artifacts of parameter choices, rather than robust forecasts about an uncertain future" For more topics to pursue in the DICE manual, see below.
2. Follow up on the references offered in the DICE manual, particularly the Ramsey model (the one that DICE is based on here) and versions of DICE that are not deterministic (here). Try to find a reference that validates the model on historical data.
3. Download the "Simple Excel" version of DICE (here and here). Try to understand the model and explore different runs. Make simple changes to the alternative assumptions. NOTE: the Excel model seems "under development" and I have not been able to get it running. Skip to Exercise 4 if you're having trouble.
4. Download the free educational version VENSIM PLE (here) and the version of DICE in the VENSIM language from Tom Fiddaman's System Dynamics Model Library, specifically here. Become familiar with the VENSIM language. Most of the causal macrosystems I will review have been implemented in VENSIM and it is free.

Using the DICE manual, evaluate and critique the following statements:

1. DICE is an optimization model. "...the use of optimization can be interpreted in two ways: First, from a positive point of view, optimization is a means of simulating the behavior of a system of competitive markets; and, second, from a normative point of view, it is a possible approach to comparing the impact of alternative paths or policies on economic welfare" (p. 6)
2. "In the DICE and RICE models, the world or individual regions are assumed to have well-defined preferences, represented by a social welfare function, which ranks different paths of consumption" (p. 6).
3. "Technological change takes two forms: economy-wide technological change and carbon-saving technological change. The level of total factor productivity ... is a logistic equation similar to that of population...TFP growth declines over time" (p. 9). This is an interesting change of specification. In the neoclassical economic growth model, TFPG is simply an exponential function, meaning it increases forever since there are no inherent limits to the growth of knowledge (see my earlier post here).
4. "...providing reliable estimates of the damages from climate change over the long run has proven extremely difficult" (p. 10 and following).
5. "The DICE-2013R model explicitly includes a backstop technology, which is a technology that can replace all fossil fuels" (p. 13).
6. "The model assumes that incremental extraction costs are zero and that carbon fuels are efficiently allocated over time by the market" (p. 14)
7. "As with the economics, the modeling philosophy for the geophysical relationships has been to use parsimonious specifications so that the theoretical model is transparent and so that the optimization model is empirically and computationally tractable" (p. 15).
8. "This discussion implies that we can interpret optimization models as a device for estimating the equilibrium of a market economy. As such, it does not necessarily have a normative interpretation. Rather, the maximization is an algorithm for finding the outcome of efficient competitive markets" (p. 22). How well does this interpretation fit the world system?
9. "The real interest rate is a critical variable for determining climate policy" (p. 25).
10. "Earlier versions of DICE and other IAMs tended to have a stagnationist bias, with the growth rate of total factor productivity declining rapidly in the coming decades. The current version assumes continued rapid total factor productivity growth over the next century, particularly for developing countries" (p. 36).
11. "The 2007 model over predicted output by about 6 percent, primarily because of failure to see the Great Recession. We have reduced output to put the new path on the current starting point" (p. 41).
12. "Since many computerized climate and integrated assessment models contain between 10,000 and 1 million SLOC...[source lines of code]..., there is the prospect of many bugs contained in our code" (p. 52).
13. "...there is a tendency to develop models that increase in parallel with the rapidly expanding frontier of computational abilities. This leads to increasingly large and complex models. We need also to ask, do we fully understand the implication of our assumptions? Is disaggregation really helping or hurting?" (p. 53)
14. "The properties of linear stochastic systems are moderately well-understood, but that is not the case of all non-linear stochastic systems" (p. 54).

Stacking the Deck at the Climate Casino

This year, Prof. William Nordhaus (Yale) published The Climate Casino: Risk, Uncertainty and Economics for a Warming World. The book continues Professor Nordhaus' forty year career investigating the economics of energy resources. The book was also recently reviewed by Paul Krugman (Princeton, here) and is interesting on many levels: the use of sophisticated macroeconomic models, attempts to forecast far out into the future, the use of probability and uncertainty (the models are purely deterministic), Prof. Nordhaus' willingness to make very specific policy recommendations (increase the price of CO2 and increase technological change in the energy sector), and finally his long running argument about the Limits to Growth.

The initial argument about the Limits to Growth grew out of Prof. Nordhaus' work on nonrenewable resources, particularly fossil fuels. The argument is captured in the causal diagram above.  A group of engineers at MIT were arguing that the depletion of nonrenewable resources would lead to economic collapse. Prof. Nordhaus countered that technological change would create substitutes that would prevent any future collapse from happening. Paul Krugman points out that Nordhaus was wrong about the specifics in his long-term forecasts (real oil prices are about twice as high as the models predicted while real coal and natural gas prices are much lower) but was right to have attempted the forecast (presumably, we should be learning from what went wrong).

In any event, the argument about nonrenewable resources has morphed into an argument about the impacts of CO2 emissions on climate change, that is, the impact of extracting fossil fuels and pumping the by-products into the atmosphere.

The new argument is summarized in the causal diagram at the left which in part, is taken from page 10 of the Climate Casino. The resource extraction issue is still lurking in the link between economic growth and CO2 emissions but technological change is now supposed to help us reduce emissions by decreasing the carbon intensity of the economy.

Nordhaus accepts the basic causal link that Economic Growth -> CO2 Emissions -> Climate Change -> Ecological Impacts. He is less certain about what will happen as a result of observable ecological impacts (sea level rise, super typhoons, water scarcity, habitat loss, coastal flooding, ocean acidification, reduction of agricultural yields, and other impacts). His major argument is that policy change is needed, but his concern is also with avoiding negative effects on economic growth. The policy measures he is most focused on are cap-and-trade systems, carbon taxes, and environmental regulation. Nordhaus is looking for a policy that will raise the price of carbon, can be universally applied and will not inhibit economic growth.

One causal link that is not presented in the summary diagram on page 10 of the Climate Casino is the link between Ecological Impacts and Economic Growth. If all the negative ecological impacts listed above actually happen, negative economic impacts (Limits to Growth) would seem to be highly likely. Possibly, this is just a matter of emphasis. Policy change is already happening and Prof. Nordhaus wants to shape the debate (stack the deck?). Aside from the political agenda, there are deeper issues that go back to the reasons Prof. Nordhaus' original long-range forecasts were off the mark.

The Climate Casino uses an embellished version of the same macroeconomic growth model used to make the original predictions (here) about nonrenewable resource allocation. If the initial forecasts were not very accurate, has anything fundamental been changed in the new version to produce better projections? Publication of the Climate Casino gives us the opportunity to look back at Prof. Nordhaus' model and his competitor's models (to include the Limits to Growth models). In future posts, I'll review chapters of the Climate Casino and look more closely at the underlying models and how they were constructed. The "deep dives" into model specifics are not particularly reassuring.

Can Biodiversity Coexist with Food Production?

Watch Balancing Costa Rica's Farming With Preservation with Nature on PBS. See more from PBS NewsHour.

To my knowledge, there are no macroeconomic models that include measures of biodiversity. From the video above, it would seem to be a major omission. It's also interesting that Costa Rica is one of the first countries to recognize that biodiversity can coexist with food production. The question for this blog is how to include such measures (how to value Nature) in macro models, a topic I'll take up in future posts.