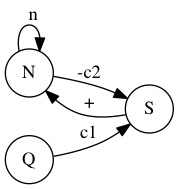
NOTES
Code
If you would like to run the R program in your web browser, cut and paste the following code into the editor window at https://rdrr.io/snippets/.
Kaya <- function (time=100,N=100,n=1.4,L=50,Q=100,q=1.04,CO2=1,
Temp=1,l=.5,e=.75,c=.0002,t=.0001,limit=1) UseMethod ("Kaya")
Kaya.default <- function (time=100,N=100,n=1.4,L=50,Q=100,q=1.04,CO2=1,
Temp=1,l=.5,e=.75,c=.02,t=.01,limit=1) {
TEMP <- matrix(0,time,1)
TIME <- matrix(0,time,1)
for (i in 1:time) {
N <- N * n;
L <- N * l; Q <- Q * q + L * e; CO2 <- Q * c; Temp <- CO2 * t; TEMP[i,1] <- Temp; TIME[i,1] <- i; if (i > time/2) {c <- c * limit} } plot(TIME,TEMP) } par(mfrow=c(2,2)) # Sample Function Calls Kaya(n=1.03,q=1.04) title(main="Exponential") Kaya(n=.9,q=1) title(main="Asymptote") # De-Growth Kaya(n=.9,q=.9) title(main="Degrowth") # Decline Kaya(n=.6,q=.6) title(main="Decline") Kaya(n=1.03,q=1.04,limit=0.95) title(main="IPCC Slow") Kaya(n=.9,q=1,limit=0.95) title(main="IPCC Fast")